


Математическа модель-
есть комплекс приближений, отвечающий нашим потребностям
Математическое моделирование
Математическая модель позволяет через систему математических соотношений — формул, уравнений, неравенств и любых других математических представлений описывать явление и исследуемый обьект.
Для описания модели используют ряд параметров, которые описывают реальный объект лишь с некоторой степенью приближения. Выделив наиболее важные факторы, можно пренебречь менее существенными.
Совокупность математических дисциплин, относящихся к организационному управлению, составляют "теорию принятия решений" или "теорию исследования операций", т.е. исследование с точки зрения повышения их эффективности.
Наиболее часто в обозначении раздела теории операций используют синонимы: теория оптимальных решений, теория принятия решений.
Типы моделей
Моделирование может быть различным и в зависимости от целей модель может использоваться:
-
для понимания явлений (как устроен конкретный объект, его свойства и взаимодействие с окружающим миром);
-
управления объектом или системой при заданных целях и критериях;
-
для прогнозирования экономических социальных и др. систем в результате воздействия на них.
По характеру предмета исследований для управления в организации можно выделить моделирование методами математического программирования в помощь для принятия решений и описания процесса, явления.
По результату закзачик получает установление количественных зависимостей или качественных, отражающих изменение каких либо характеристик с заданной точностью, описывающих объект.
Модель для принятия решений
В помощь при принятии управленческих решений используют моделирование, описывающие поведение организации, технологического процесса и другие изменения состояний при реализации определенного управленческого решения (к примеру изменения финансирования на модернизацию).
Модели принятия решений, изучаемые теорией оптимизации можно охарактеризовать кратко в алгоритме, как: ЛПР выбирает свою стратегию (решение) из заданного множества критериев S при заданной функци полезности f (s) , которая отражает интересы ЛПР и зависит от s.
Задача принятия решений записывается как:
найти такое решение s*, которое будет доставлять максимум функции f (s) при sЄS.
Классические модели принятия решений всегда являются оптимизационными, так как нацелены на максимизацию выгоды или прибыли. Они построены таким образом, чтобы можно было использовать оптимизационный алгоритм и получить оптимальную практическую рекомендацию.
Методика построения моделей
В процессе подготовки к созданию математической модели мы выделяем предположения, на которых будет основываться математическая модель и определяем, что считать исходными данными, результатами и критериями. Затем записываем или предпологаем математические соотношения, связывающие результаты с исходными данными.
Далеко не всегда удается найти формулы, явно выражающие искомые величины через данные. В таких случаях используются математические методы, позволяющие дать ответы той или иной степени точности.
Для решения задач оптимизации - нахождения наилучших вариантов из всех возможных применяются численные методы математического программирования.
Наиболее эффективно математическую модель можно реализовать на компьютере в виде алгоритмической модели — так называемого "вычислительного эксперимента", пользуясь, к примеру, средствами MATLAB.
Окончательную проверку построенной модели может дать натурный эксперимент с приближенными к реальным условиям использования обьекта, описываемого данной моделью или рассматриваемого явления.
В случае неудачи, результаты вычислительного эксперимента могут оказаться и не соответствующими действительности, если в модели не будут учтены какие-то важные стороны действительности. Для этого учитываются дополнительные параметры и эксперимент повторяется.
В том или ином случае всегда нужно помнить об адекватности модели и разумной простоты моделирования - провести с приемлемой точностью в сжатые сроки и экономично по затратам труда и средств анализ исследуемых свойств объекта, осмыслить результат и подготовить отчет. Отметим, что любая полученная модель адекватна в рамках заданных ограничений применимости модели. Распространение на все случаи жизни может привести к неточным и искаженным результатам моделирования реальных объектов.
 Снимок экрана от 2015-11-19 17_40_13_1.png |  Снимок экрана от 2015-11-19 17_40_28_1.png | 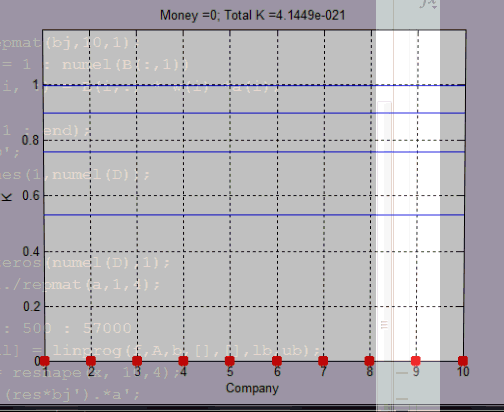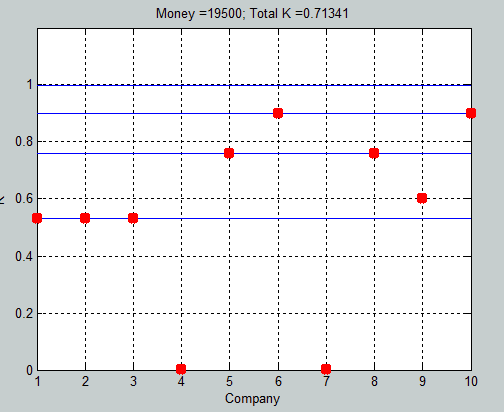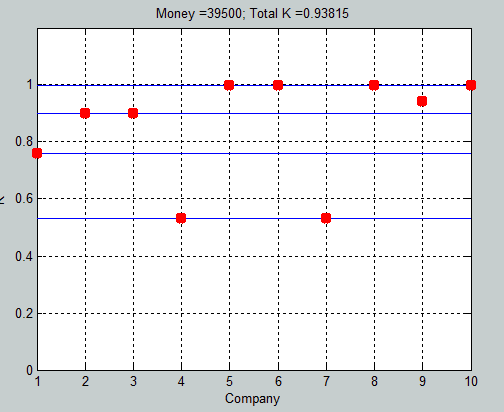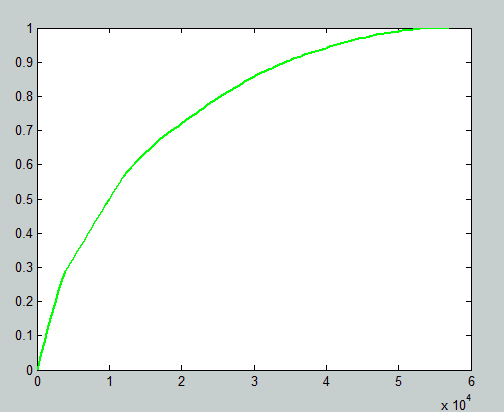 Оптим._распред. средств_для 10 ти предпр для Ка=100_запуск из браузера .gif |
|---|---|---|
 070510_1-over-f-noise-hirez.jpg |  pic3_optim.gif |
Этапы практической реализации построения любой математической модели:
-
Постановки задачи - определение ограничений, критериев, зависимых и независимых параметров в вербальной (словесной) форме.
-
Формализации - описания постановки задачи в виде определенного набора математических или логических выражений, создание алгоритмов поиска наилучшей альтернативы (для нормативных моделей) или расчета параметров (для имитационных моделей)
-
Верификации - проверки модели на адекватность реальному миру (чаще всего статистическим данным) или на полезность ее при принятии управленческих решений.
-
Применение - использование модели для подготовки и принятия управленческих решений;
-
Модернизации и корректировки - изменение описания модели по результатам ее применения, а также под воздействием изменения самой организации и среды, в которой она функционирует.
Существует не только математическое моделирование какого-либо явления, но и визуально-натурное моделирование, которое обеспечивается за счет отображения этих явлений средствами машинной графики.